2023
Estudiantes y Representantes Marquenses:
Reciban mi mas cordial saludo. Mi nombre es Javier Estrella y soy el profesor asignado a las materias de Matemáticas y Física.
Esta plataforma ayuda al control diario de la asignatura tanto para el mismo estudiante como para los Padres de familia o Representantes.
Debemos considerar que el Rectorado tiene acceso total a este contenido.
En esta modalidad a distancia recibirán mis llamadas , video llamadas y mensajes de whatsapp únicamente dentro del horario asignado por la UESM (UNIDAD EDUCATIVA SAN MARCOS).
Los deberes, trabajos grupales o individuales, exposiciones grabadas, e investigaciones serán entregados a la siguiente e-mail: javierestrella11@gmail.com
En la realización de trabajos digitales esta prohibido COPIAR Y PEGAR. Para lo cual, utilizaremos OBLIGATORIAMENTE la técnica de PARAFRASEAR así como también se incentivará a que el estudiante pueda CREAR su propio contenido.
Las dudas e inquietudes referentes a la Asignatura serán recibidas y contestadas vía whatsapp.
De aquí en adelante, lo realizaremos todo en hojas cuadriculadas y lo llevaremos en una carpeta de cartón (manila) con binchas que deberá incluir como primera hoja su respectiva CARÁTULA, la misma que también tiene puntaje.
La elaboración de las fichas nemotécnicas son de carácter obligatorio.
El tamaño de las fichas nemotecnicas es uniforme para todos. Por ejemplo, Para obtener dos fichas nemotécnicas tomamos una lámina de cartulina blanca A4, la doblamos por la mitad y cortamos Y ASI OBTENDREMOS DOS FICHAS DE CADA LÁMINA A4
Muchas gracias.
Empecemos......
Para Dar inicio a la primera clase, en este punto ya estará hecha la carátula en la primera hoja de nuestra carpeta manila.. y en la siguiente hoja ponemos:
como título: TERCER TRIMESTRE.
como subtitulo: LOS NÚMEROS Y EL PLANO CARTESIANO
FECHA: JUEVES 14 DE SEPTIEMBRE DEL 2023
Números naturales
Con los números naturales contamos los elementos de un conjunto (número cardinal). O bien expresamos la posición u orden que ocupa un elemento en un conjunto (ordinal).
El conjunto de los números naturales está formado por:
N= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...}
Números naturales
Con los números naturales contamos los elementos de un conjunto (número cardinal). O bien expresamos la posición u orden que ocupa un elemento en un conjunto (ordinal).
El conjunto de los números naturales está formado por:
N= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...}
Números ENTEROS
Los números enteros son del tipo:
= {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}
Nos permiten expresar: el dinero adeudado, la temperatura bajo cero, las profundidades con respecto al nivel del mar, etc.
Los números enteros son del tipo:
= {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}
Nos permiten expresar: el dinero adeudado, la temperatura bajo cero, las profundidades con respecto al nivel del mar, etc.
Números racionales
Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero.
Los números decimales (decimal exacto, periódico puro y periódico mixto) son números racionales; pero los números decimales ilimitados no.
Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción.
El número irracional más conocido es 
, que se define como la relación entre la longitud de la circunferencia y su diámetro.
= 3.141592653589...
Otros números irracionales son:
El número e aparece en procesos de crecimiento, en la desintegración radiactiva, en la fórmula de la catenaria, que es la curva que podemos apreciar en los tendidos eléctricos.
e = 2.718281828459...
El número áureo, 
, utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus obras.
Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero.
Los números decimales (decimal exacto, periódico puro y periódico mixto) son números racionales; pero los números decimales ilimitados no.
Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción.
El número irracional más conocido es , que se define como la relación entre la longitud de la circunferencia y su diámetro.
= 3.141592653589...
Otros números irracionales son:
El número e aparece en procesos de crecimiento, en la desintegración radiactiva, en la fórmula de la catenaria, que es la curva que podemos apreciar en los tendidos eléctricos.
e = 2.718281828459...
El número áureo, , utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus obras.
Números reales
El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por 
.
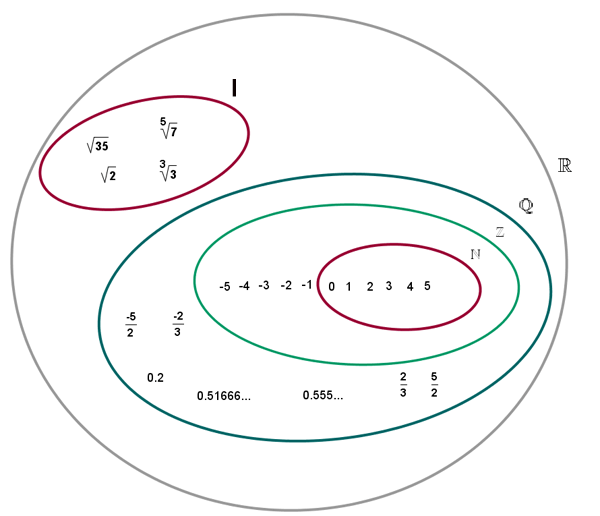
Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo y la división por cero.
El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por .
Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo y la división por cero.
La recta real
A todo número real le corresponde un punto de la recta y a todo punto de la recta un número real.
A todo número real le corresponde un punto de la recta y a todo punto de la recta un número real.
Números imaginarios
Un número imaginario se denota por bi, donde :
b es un número real
i es la unidad imaginaria: 
Los números imaginarios permiten calcular raíces con índice par y radicando negativo.
x2 + 9 = 0
Un número imaginario se denota por bi, donde :
b es un número real
i es la unidad imaginaria:
Los números imaginarios permiten calcular raíces con índice par y radicando negativo.
x2 + 9 = 0
Números complejos
El conjunto de los números complejos se puede ejemplarizar mediante
Un número complejo en forma binómica como lo es a + bi.
El número a es la parte real del número complejo.
El número b es la parte imaginaria del número complejo.
Si b = 0 el número complejo se reduce a un número real, ya que a + 0i = a.
Si a = 0 el número complejo se reduce a bi, y se dice que es un número imaginario puro.
EL PLANO CARTESIANO
PASAR HASTA AQUI. ADICIONALMENTE, TODA EXPLICACION DE CLASE VA A LA CARPETA EN EL LIBRO.- REALIZAR DESTREZAS PAG.15, NUMERALES 4,5,6 Y 7. --------------------------------------------------------------------------------fin de la clase MARTES 19EN EL LIBRO.- LEER DETENIDAMENTE.- VALOR ABSOLUTO DE LOS NUMEROS , PAG 16EN LA CARPETA.- REALIZAR DESTREZAS PAG.17, NUMERALES 3 Y 4. --------------------------------------------------------------------------------fin de la claseMIERCOLES 20EN EL LIBRO.- LEEMOS DETENIDAMENTE.- ORDEN DE LOS NUMEROS , PAG 18EN LA CARPETA.- REALIZAR DESTREZAS PAG.19, NUMERALES 2,3,4,5,6,7,8--------------------------------------------------------------------------------fin de la clase
HACER LAS DOS FICHAS NEMOTECNICAS QUE ESTAN EN EL REPASO 16 DE BASES. (VALE 2PTS.)ATENTOS A LA CLASE EXPLICATIVA... Y PREGUNTA A TU PROFESOR SOBRE LA LEY DE SIGNOSLUNES 25LEEMOS DETENIDAMENTE.- ADICION O SUMA DE LOS NUMEROS , PAG 20EN EL LIBRO.- REALIZAR DESTREZAS PAG.22, NUMERALES 2 Y 3-------------------------------------------------------------------------------------------------MARTES 26DIA DE LA BANDERA-------------------------------------------------------------------------------------------------MIERCOLES 27FICHA NEMOTÉCNICA DE LAS TABLAS DE MULTIPLICAR
ESTA FICHA NEMOTECNICA LA HACEMOS EN CARTULINA. PARA ELLO TOMAREMOS UN LÁMINA
DE CARTULINA A4 Y LA PARTIMOS POR LA MITAD, Y YA ESTA! TENEMOS PARA DOS FICHAS..
EN UNA DE ELLAS PEGAMOS O HACEMOS A MANO EL CUADRO DE LAS TABLAS, Y LO
TRATEREMOS DE LEER MUCHAS VECES Y A RATOS CON LOS OJOS CERRADOS..
VAMOS!
LEEMOS DETENIDAMENTE.- RESTA O SUSTRACCION DE LOS NÚMEROSENTEROS , PAG 24EN EL TEXTO.- REALIZAMOS DESTREZAS PAG.25 NUMERALES 1, 2, Y 3
------------------------------------------------------------------------------------FIN DE CLASE
LUNES 2 DE OCTUBRE
LES RECUERDO QUE PARA EL APORTE, SERÁN EJERCICIOS Y PREGUNTAS EXTRAÍDAS
DEL LIBRO DE EJERCICIOS 8.
TAREA DE CLASE.- RESOLVEMOS EN EL LIBRO DE EJERCICIOS
LO SGTE.:PAG 20 A 23.
REPASO PREVIO AL APORTE.-
ORDEN DE LOS NÚMEROS EN LA RECTA,
LA RECTA NUMÉRICA
LOS PARES ORDENADOS Y EL PLANO CARTESIANO
SUMAS Y RESTAS (USANDO LEY DE SIGNOS)
MULTIPLICACIONES Y DIVISIONES (USANDO LEY DE SIGNOS)
-------------------------------------------------------------------------------------------fin de la clase
El conjunto de los números complejos se puede ejemplarizar mediante
Un número complejo en forma binómica como lo es a + bi.
El número a es la parte real del número complejo.
El número b es la parte imaginaria del número complejo.
Si b = 0 el número complejo se reduce a un número real, ya que a + 0i = a.
Si a = 0 el número complejo se reduce a bi, y se dice que es un número imaginario puro.
EL PLANO CARTESIANO
ESTA FICHA NEMOTECNICA LA HACEMOS EN CARTULINA. PARA ELLO TOMAREMOS UN LÁMINA
DE CARTULINA A4 Y LA PARTIMOS POR LA MITAD, Y YA ESTA! TENEMOS PARA DOS FICHAS..
EN UNA DE ELLAS PEGAMOS O HACEMOS A MANO EL CUADRO DE LAS TABLAS, Y LO
TRATEREMOS DE LEER MUCHAS VECES Y A RATOS CON LOS OJOS CERRADOS..
VAMOS!
------------------------------------------------------------------------------------FIN DE CLASE
LUNES 2 DE OCTUBRE
LES RECUERDO QUE PARA EL APORTE, SERÁN EJERCICIOS Y PREGUNTAS EXTRAÍDAS
DEL LIBRO DE EJERCICIOS 8.
TAREA DE CLASE.- RESOLVEMOS EN EL LIBRO DE EJERCICIOS
LO SGTE.:PAG 20 A 23.
REPASO PREVIO AL APORTE.-
ORDEN DE LOS NÚMEROS EN LA RECTA,
LA RECTA NUMÉRICA
LOS PARES ORDENADOS Y EL PLANO CARTESIANO
SUMAS Y RESTAS (USANDO LEY DE SIGNOS)
MULTIPLICACIONES Y DIVISIONES (USANDO LEY DE SIGNOS)
-------------------------------------------------------------------------------------------fin de la clase
Lo que se encuentra bajo esta línea roja no no pertenece a tu clase actual.
--------------------------------------------------------------------------------------------------------------
TEMAS CENTRALES DE ESTUDIO MATEMÁTICO DE OCTAVO AÑO DE EGB.
VALOR ABSOLUTO DE LOS NUMEROS ENTEROS p16. deber p17 (3,4,5,6)
ORDEN DE LOS NUMEROS ENTEROS. p18. Deber p.19 (2,3,4,5)
ADICION Y SUSTRACCION DE ENTEROS. p 20, 21, 24,25. Deber p22(2,3,4); p25 (2,3,4)
IGUALDADES, ECUACIONES E INECUACIONES p26,27,28. Deber p29 (2,3,4)
MULTIPLICACION DE NUMEROS ENTEROS. p36,37. Deber p38( 2,3,6,7,9,10 Y 15)
ECUACIONES CON ESTRUCTURA MULTIPLICATIVA. p.42y 43. Deber 43 (3,4,5)
OPERACIONES COMBINADAS CON ENTEROS Y JERARQUIA. p.44,45,46. Deber p.46 (2,3,4)
POTENCIAS Y OPERACIONES CON POTENCIAS. p.48,49,50. Deber p.51 (3,4,5)
RAICES CUADRADAS Y OPERACIONES.p.52,53. Deber p.54 (2,3,4)
LOS NUMEROS RACIONALES ( FRACCIONES, DECIMALES, PORCENTAJES) p68 y 69.
EXPRESION DECIMAL DE LOS NUMEROS RACIONALES. p70,71. Deber p71 (2,3,4)
FRACCION GENERATRIZ p72,73,74
NUMEROS RACIONALES EN LA RECTA NUMERICA. p 76 ,77
RELACION DE ORDEN DE LOS NUMEROS RACIONALES 78,79
ADICION DE NUMEROS RACIONALES Y SUS PROPIEDADES. p80 81,82 Deber p 82 (2,5,6,7,9)
SUSTRACCION DE NUMEROS RACIONALES Y SUS PROPIEDADES. p84 85 Deber p 85 (2,3,5)
ECUACIONES CON NUMEROS RACIONALES. p.92. Deber p.93 (2,3,5,6,7)
POTENCIACION DE NUMEROS RACIONALES p94,95,96. Deber p97 (2,3,5)
RADICACION DE NUMEROS RACIONALES p98,99,100. Deber p 101 (2,3,5)
OPERACIONES COMBINADAS CON NUMEROS RACIONALES. p102,103 Deber p103 (2y3)
TEMAS CENTRALES DE ESTUDIO GEOMÉTRICO
POLIEDROS
PRISMAS
PIRÁMIDES
POLIEDROS REGULARES
CUERPOS REDONDOS
POLIGONOS
CUADRILATEROS
FIGURAS CONGRUENTES Y SEMEJANTES
TEOREMA DE TALES
HEMOTECIAS
PERIMETRO DE FIGURAS PLANAS
UNIDADES DE SUPERFICIE
AREA DE FIGUAS PLANAS
TEOREMA DE PITAGORAS
AREA DE POLIGONOS REGULARES
LONGITUDES Y AREAS DE FIGURAS CIRCULARES
AREA DE PRISMAS Y PIRAMIDES
AREA DE CILINDROS Y CONOS
BLOQUE COMPLEMENTARIO
PROPOSICIONES
NUMEROS Y LETRAS, LENGUAJE ALGEBRAICO
EXPRESIONES ALGEBRAICAS.
SISTEMA DE COORDENADAS CARTESIANAS.
FUNCIONES
FUNCIONES DE PROPORCIONALIDAD DIRECTA E INVERSA.
.
_____________________________________________________________________
_____________________________________________________________________
Teorema de Pitágoras
El Teorema de Pitágoras es un teorema que nos permite relacionar los tres lados de un triángulo rectángulo, por lo que es de enorme utilidad cuando conocemos dos de ellos y queremos saber el valor del tercero.
También nos sirve para comprobar, conocidos los tres lados de un triángulo, si un triángulo es rectángulo, ya que si lo es sus lados deben cumplirlo.
Como ya sabréis, un triángulo rectángulo es aquél en el que uno de sus tres ángulos mide 90 grados, es decir, es un ángulo recto. Está claro que si uno de los ángulos es recto, ninguno de los otros dos puede serlo, pues deben sumar entre los tres 180 grados.
En los triángulos rectángulos se distinguen unos lados de otros. Así, al lado mayor de los tres y opuesto al ángulo de 90 grados se le llama hipotenusa, y a los otros dos lados catetos.
Pues bien, el Teorema de Pitágoras dice que: «En todo triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos«.
Si lo expresamos de forma geométrica, el Teorema de Pitágoras quiere decir que el área de un cuadrado de lado la hipotenusa es igual a la suma de las áreas de otros dos cuadrados cuyos lados son cada uno de los catetos respectivamente.
Existen muchas demostraciones del Teorema de Pitágoras. Como ejemplo podéis ver esta pequeña animación de tan solo un minuto en la que se muestran seis demostraciones geométricas, o esta otra con piezas de lego.
Vamos a ver una aplicación práctica del Teorema de Pitágoras para calcular un lado desconocido en un triángulo rectángulo.
Se quiere sujetar un poste vertical de 5 metros de altura con un cable tirante desde su parte más alta hasta el suelo. Si la distancia desde el punto de anclaje del cable en el suelo a la base del poste es de 12 metros, ¿cuánto debe medir el cable?
Como el poste vertical es perpendicular al suelo, forma un ángulo recto con él. Si consideramos el propio poste, el cable y la distancia entre la base del poste y el punto de anclaje al suelo, tenemos un triángulo rectángulo:
Llamando x a la longitud del cable, y aplicando el Teorema de Pitágoras, se debe cumplir que:
Es decir, el cable debe medir 13 metros.
Antes de seguir, quiero dejar claro que, la ecuación de segundo grado incompleta anterior tendría dos posibles soluciones, 13 y -13, pero al tratarse de longitudes, no tiene sentido el resultado negativo, por lo que solo he tenido en cuenta directamente el positivo. Esto es algo que haremos siempre al utilizar el Teorema de Pitágoras.
Veamos otro ejemplo donde lo que queramos calcular no sea la hipotenusa si no uno de los dos catetos.
Una escalera de 2,5 metros de longitud está apoyada en una pared vertical. Si el pie de la escalera está colocado a medio metro de dicha pared, ¿a qué altura llega la parte superior de la escalera?
Al ser la pared vertical, la pared y el suelo son perpendiculares. Si consideramos la escalera, la altura que alcanza ésta en la pared medida desde el suelo, y la distancia del pie de la escalera a la pared, tenemos un triángulo rectángulo:
Llamando h a la altura que alcanza la escalera en la pared, y aplicando el Teorema de Pitágoras, se tiene que:
La escalera llega a una altura de 2,45 metros.
En los dos ejemplos que hemos visto hasta ahora formamos directamente un triángulo rectángulo, pero en muchas ocasiones la figura inicial es otra, y la construcción del triángulo rectángulo la hacemos para poder calcular alguna medida desconocida de ésta.
En el siguiente ejemplo tenemos un trapecio y vamos a utilizar un triángulo rectángulo para calcular uno de sus lados:
Calcula el perímetro del siguiente trapecio rectángulo:
El perímetro del trapecio es igual a la suma de las longitudes de sus cuatro lados. Para calcularlo necesitamos primero calcular la longitud del lado inclinado, que desconocemos.
Llamando x al lado desconocido, podemos considerar el triángulo rectángulo que se muestra en la siguiente figura:
Tenemos, por tanto, un triángulo rectángulo de hipotenusa x y catetos de 15 y 10 cm. Aplicando el Teorema de Pitágoras:
El lado del trapecio que nos faltaba por saber mide 18,03 cm, por lo que el perímetro será:
El perímetro del trapecio es de 83,03 cm.
Por último, os voy a poner un ejemplo de la otra posible aplicación que os comentaba al comienzo que tiene el teorema de Pitágoras: comprobar, conocidos los tres lados de un triángulo, si es un triángulo rectángulo o no.
Comprueba si los siguientes segmentos forman triángulos rectángulos:
a) 25 cm, 24 cm, 7 cm.
b) 12 cm, 15 cm, 4 cm.
Vamos con el primero.
Si es un triángulo rectángulo, se debe cumplir que el cuadrado del mayor de los tres segmentos sea igual a la suma de los cuadrados de los otros dos segmentos.
El cuadrado del segmento de mayor longitud (el segmento de 25 cm) es:
Y la suma de los cuadrados de los otros dos segmentos es:
Como podemos observar, se cumple el Teorema de Pitágoras y, por tanto, podemos afirmar que los segmentos de 25 cm, 24 cm y 7 cm forman un triángulo rectángulo.
Veamos ahora el segundo:
El cuadrado del segmento de mayor longitud, que en este caso es el segmento de 15 cm, es:
Y la suma de los cuadrados de los otros dos segmentos es:
No son iguales, por lo que no se cumple el Teorema de Pitágoras y, en consecuencia, el triángulo que forman los segmentos de 12 cm, 15 cm y 4 cm no es rectángulo.
De hecho podemos afirmar que dichos segmentos forman un triángulo obtusángulo (tiene uno de sus ángulos obtusos, es decir, mayor de 90 grados).
¿Por qué lo se?
Es muy sencillo. Se cumple siempre que:
Si el cuadrado del lado de mayor longitud es mayor que la suma de los cuadrados de los otros dos lados se trata de un triángulo obtusángulo (triángulo con un ángulo obtuso, mayor de 90 grados).
Si el cuadrado del lado de mayor longitud es igual que la suma de los cuadrados de los otros dos lados es un triángulo rectángulo (es lo que dice el Teorema de Pitágoras).
Y, si el cuadrado del lado de mayor longitud es menor que la suma de los cuadrados de los otros dos lados se trata entonces de un triángulo acutángulo (triángulo con los tres ángulos agudos, menores de 90 grados).
Espero que todo esto que os he contado os haya gustado y os sea útil.
Y recordad una cosa: El Teorema de Pitágoras solo se cumple en triángulos rectángulos, así que si el triángulo no es rectángulo no lo podemos utilizar.
